
AD-GS:稀疏视角 3D Gaussian Splatting 的“交替致密化”,同时抑制浮游物与保留细节
一句话版结论
AD-GS 的核心是把 3DGS 的“致密化(densification)”做成高/低两个相互交替的阶段:
- 高致密化:用更宽松的阈值积极分裂/克隆高残差区域的高斯,专注恢复高频细节(仅用光度损失训练);
- 低致密化:用更严格的阈值放缓致密化并强力剪枝(高不透明度阈值),同时加入伪视角一致性 + 边缘感知的深度平滑两种几何正则,专注几何稳定与抑制浮游物(floaters)。
两相交替,既避免一味致密导致的“漂浮伪结构”,又避免全程强正则带来的过度平滑与细节丢失。
1. 背景:为什么稀疏视角下 3DGS 容易“翻车”
经典 3DGS 在多视角密集监督下很强,但输入视角稀疏时会出现:
- 浮游物(floaters):不在真实表面上的错误高斯,常出现在致密化随机分裂后;
- 几何不准 & 过拟合:受限观察导致“就近拟合”训练视图,跨视角一致性差;
- 不受控致密化:分裂/克隆容易把高斯“撒偏”,后续还会围绕它继续增殖,问题滚雪球。
AD-GS 的目标,就是在不引入外部深度先验的前提下,仅靠训练机制设计,抑制浮游物并保细节。
2. 方法概览:交替致密化(Alternating Densification)

训练由三个阶段按周期交替进行(两套 3DGS 模型并行训练,用于后续的一致性约束):
-
Warm-Up 预热:仅用光度损失(L1 + SSIM)分别训练两套模型,得到稳定初始化。
-
低致密化阶段(Low-Dfn,几何整形)
-
强剪枝:提高不透明度阈值,去除低 α 的可疑高斯;
-
慢致密:提高梯度阈值,放缓克隆/分裂;
-
几何正则(本阶段才启用)
- 伪视角一致性:对训练视角的小扰动视角,约束两模型渲染结果一致;
- 边缘感知深度平滑:在纹理平坦处鼓励深度光滑,在图像边缘保留深度突变;
-
-
高致密化阶段(High-Dfn,细节恢复)
- 快致密:回到较低的梯度阈值,积极克隆/分裂补细节;
- 仅光度损失:拿掉几何正则,避免过平滑影响细节生长。
关键设计:几何正则只在低致密化阶段使用。若全程使用,会抑制细节(论文对比 CoR-GS 的平滑问题即源于此)。
3. 损失函数与优化要点
- 光度损失(训练视角):
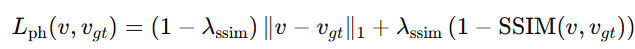
- 伪视角一致性(两模型间,伪视角渲染 u):
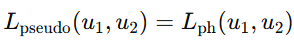
- 低致密化阶段的总损失:
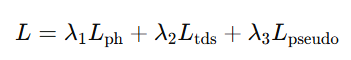
高致密化阶段仅用
- 训练流程(伪代码)
# 两套模型 G1, G2;循环交替执行
for phase in training_schedule:
if phase == "warmup":
# 仅光度损失
train(G1, loss=L_ph); train(G2, loss=L_ph)
elif phase == "low_densify":
# 强剪枝 + 慢致密
prune_with_high_alpha_threshold(G1); slow_densify(G1)
prune_with_high_alpha_threshold(G2); slow_densify(G2)
# 几何正则:伪视角一致 + 边缘感知深度平滑
u = make_pseudo_view(perturb(train_view))
train(G1, loss=L_ph + L_tds(G1,u) + L_pseudo(G1,G2,u))
train(G2, loss=L_ph + L_tds(G2,u) + L_pseudo(G1,G2,u))
elif phase == "high_densify":
# 快致密(积极克隆/分裂),仅光度
fast_densify(G1); train(G1, loss=L_ph)
fast_densify(G2); train(G2, loss=L_ph)
实现提示:
slow_densify/fast_densify通过梯度范数阈值控制;prune_with_high_alpha_threshold用更高 α 阈值清除半透明“浮游物”;- 伪视角
u可对训练相机做小幅位姿扰动生成。
5. 与相关工作对比(稀疏视角场景)
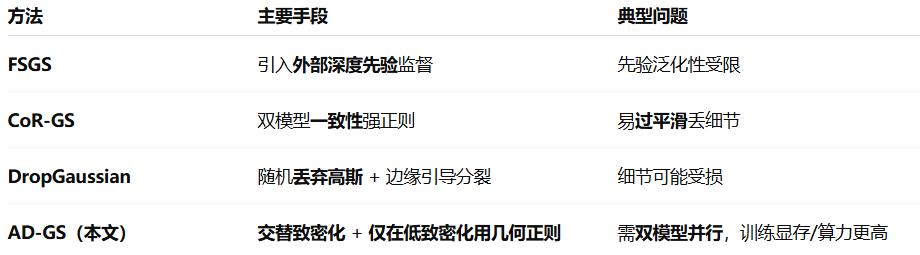
AD-GS 的创新在于:不依赖外部深度,只靠训练节律和损失编排,就能兼顾细节与几何稳定。
6. 结果速览(代表性数字)
- LLFF(3 视角):SSIM 0.699(CoR-GS 0.674;DropGaussian 0.674/0.266→LPIPS 0.237),细节 & 感知质量均提升;
- Tanks&Temples(9 视角):LPIPS 0.113(优于 3DGS/CoR-GS/DropGaussian),同时 PSNR/SSIM 更高;
- Mip-NeRF360(12 视角):SSIM 0.593(高于 CoR-GS 0.579、DropGaussian 0.575)。
7. 消融结论
- 去掉交替致密化 → SSIM 明显下降,说明“快慢结合”的必要性;
- 去掉交替损失(几何正则) → 深度图噪声与结构差,浮游物难抑;
- 全程都用几何正则 → 细节恢复受抑(过正则化)。
最佳实践就是论文主张的“阶段性几何正则 + 阶段性激进致密”。
8. 复现与落地建议
-
双模型并行:保证显存,或降低分辨率/批量。
-
阈值与节律:
- 高/低致密化的迭代配比与梯度阈值是关键调参点;
- 低致密阶段α 剪枝宜更激进;
-
伪视角生成:对训练视角做小扰动(平移/旋转少量),避免与训练分布偏离过远;
-
损失权重:
-
工程化:把致密化与剪枝封装成策略类,便于切换“高/低模式”;深度平滑用渲染深度直接计算梯度即可。
9. 局限与展望
- 资源开销:双模型训练增加显存与算力;
- 一致性“共错”问题:两模型若在伪视角上犯“同类错误”,一致性约束难以纠偏;
- 事后纠偏:当前更多是“致密后再纠正”,未来可研究几何一致的致密化策略,甚至学习型自适应致密化调度。
10. 给不同读者的快速建议
- 做应用/比赛:把 AD-GS 当作稳健化外壳套在 3DGS 训练外层,用默认节律先跑基线,优先调“高/低阶段时长 + 剪枝阈值”。
- 做研究:可沿“致密化策略学习”“可变节律调度”“与生成先验(扩散/分割/法线)结合”三条线深入。
结语
AD-GS 用简单而有效的训练节律设计,把稀疏视角 3DGS 中“细节恢复”和“几何稳定”这对老难题,做到了同向提升。如果你在少视角、含弱纹理场景里一直被浮游物和过平滑折磨,不妨把“交替致密化 + 阶段性几何正则”的套路搬进你的代码仓。
参考论文:AD-GS: Alternating Densification for Sparse-Input 3D Gaussian Splatting(ACM TOG,2025,arXiv:2509.11003)
